The magnetic field exerts force exerts force on other moving charges or electric currents not on stationary charges. That's because a moving charge has magnetic field. Not only a magnet (magnetic field) exerts force on a current, the current also exerts the force on the magnet (by Newton's third law).
The phenomenon of a current exerting force on magnet was first observed by Oersted (compass needle was deflected by current). Current in a conductor means flow of charges.
Let's consider a current carrying conductor (wire) of length \(l\) and cross-sectional area \(A\) (Figure 1). The drift velocity of charges flowing in the conductor is \(v_d\). You know from the expression for the magnetic force on a charge \(q\), \(\vec F = q\vec v \times \vec B\), that is \(F = qvB\sin \theta\).

If \(n\) is the charge per unit volume (concentration) of charges, then the total charge within the length of the conductor is \(nAl\), so the magnetic force on the conductor is
\[F = nAlqv_dB\sin \theta\]
where \(\theta\) is the angle between the magnetic field and the conductor (if the magnetic field makes an angle other than \(90^\circ\) with the conductor). You know the expression of electric current, that is \(I = nqAv_d\), so
\[F = IlB\sin \theta = I \vec l\times \vec B \tag{1} \label{1}\]
The direction of magnetic force is again given by the right hand thumb rule of cross product of vectors. All you have to do is curl the fingers in the direction of in the sense of \(\vec l\) moving into \(\vec B\) keeping the thumb straight up and the thumb gives the direction of force for positive moving charge. If the moving charge is negative, the direction is opposite to the direction of \(\vec l \times \vec B\).
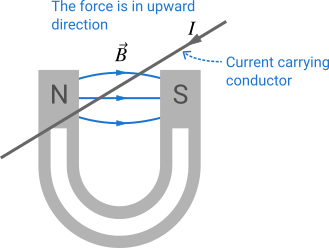

The direction of current is always the direction of flow of positive charge, that is which way the flow of positive charge is directed. While saying the direction of current, you never think that current is a vector quantity.
Note that in a straight current carrying conductor, the length vector \(\vec l\) is directed towards the direction of the flow of positive charge. So, in above figures Figure 1 and Figure 2 you can apply the right hand rule to determine the force to be upward or downward. If the wire is curved, the current is the same regardless of direction but the element of length vector \(d\vec l\) changes direction (it is always tangent to the curve).

In Figure 4 you can see a curved conductor in magnetic field in which the direction of force is directly towards you out of the web page (guessing you are reading in a computer screen or smart phone).
To determine the total force on the the curved conductor, we take the small length element in the conductor \(d \vec l\) and the small magnetic force is \(dF = IdlB\sin\theta\). Now you integrate for the entire length to find the total force
\[ F = I\int dl\,B\sin \theta \tag{2} \label{2}\]
Using above equation, you can determine the magnetic force on any shaped conductor in magnetic field. You'll soon see that the magnetic force on a curved conductor is the same as the magnetic force on a straight conductor joining the two endpoints of the curve.
Using Equation \eqref{1} you can also determine the magnetic field \(\vec B\) by measuring the force on a current carrying conductor and hence that equation is considered as the alternative definition of magnetic field. The expression of the magnetic field is determined by the Biot-Savat law based on experiments and Equation \eqref{1} is completely valid with the expression of \(\vec B\).
What is magnetic force on a curved conductor (semicircle)?
In Figure 5 you can see a semicircular conductor where the magnetic field is perpendicularly outward from the plane of the semicircular conductor of radius \(R\). The current \(I\) exists in the conductor and the conductor experiences magnetic force. To determine the magnetic force on a curved conductor, we consider the conductor as the combination of infinitesimally small elements of length \(dl\) and integrate over the whole curved length.

We have two segments in the semicircular conductor; one is the straight conductor and another is the curved conductor. For the straight portion of the conductor, you can also use Equation \eqref{1} but we use Equation \eqref{2} for consistency (the conductor does not only have straight segment) here.
\[\vec F_1 = I \int ^{R}_{-R} d\vec l \times \vec B =-2IRB \, \hat j\]
Now on the curved portion of the conductor, the small force \(d\vec F_2\) on the small element \(d\vec l\) is
\[d\vec F_2 =I d\vec l \times \vec B = I\,dl\,B\sin \theta \, \hat j \]
The magnetic field \(\vec B \) and \(d\vec l\) are always perpendicular to each other and therefore the angle \(\theta\) is always \(90^\circ\). So the magnitude of force \(d\vec F_2\) is \(I\,dl\,B\). You know that \(dl = R\,d\theta\), so the x-component of \(d\vec F_2\) is \(IRBd\theta \cos \theta\,\hat i\) and the y-component is \(IRBd\theta \sin \theta \, \hat j\). Now to find the total x and y-components we integrate from \(0\) to \(\pi\), that is
\[\vec F_{2x} = IRB\int^\pi_0 \cos \theta \, d\theta \, \hat j = 0\]
\[\vec F_{2y} = IRB\int^\pi_0 \sin \theta \, d\theta \, \hat j = 2IRB \, \hat j\]
It is assumed that you know every step of the integration process, so the final result is shown. Electromagnetism is mathematically demanding and you must know integration! So, the total force \(\vec F_2\) is \(2IRB\,\hat j\).
The interesting result here is that if you sum \(\vec F_1\) and \(\vec F_2\), the result is zero, that is we can conclude that the total magnetic force in a closed loop in a uniform magnetic field is zero. Another fact you may have noticed is that the magnetic force on the curved portion of the conductor is the same as the magnetic force on the straight conductor joining the endpoints of the curved conductor.





