You may be quiet familiar with friction in everyday life. It has both advantages and disadvantages. For example you can walk on the ground due to the friction between the surfaces of your feet and floor. But different parts of machines may not work properly due to friction which you can fix by lucubrating oils such as grease or something else. But still you can not imagine the world without friction. Here we discuss about static and kinetic friction forces.
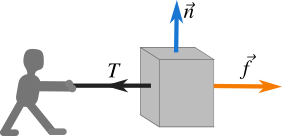
In Figure 1 a person pulls a box with a rope. The box does not move initially which is due to the friction between the surfaces of the box and the floor. And as he goes on increasing the force on the rope or the tension \(T\), the box just starts to move at a particular point called critical point. The friction before the box in motion is called static friction. The maximum value of static friction is the maximum force at which the box just starts to move.
The total force applied by the person until the box just starts to move is balanced by the corresponding static friction (maximum static friction) between the surfaces of box and the floor. Experiments have shown that the static friction is directly proportional to the normal force on the box, that is \({{f}_{s}}\propto n\) where \({{f}_{s}}\) is the static friction and \(n\) is the normal force. The maximum value of the static friction is
\[{{f}_{s-\max }}={{\mu}_{s}}n \tag{1} \label{1}\]
In Eq. \eqref{1} \({{\mu}_{s}}\) is a constant called coefficient of static friction. The value of static friction can vary from zero to a maximum value and \({{f}_{s}}\) represents any value from zero to maximum. But \eqref{1} is valid only for maximum value of static friction otherwise the coefficient of static friction will be no longer be constant as indicated by \({{\mu }_{s}}=\frac{{{f}_{s}}}{n}\).
After the maximum static friction is overcome by the applied force, the box starts to move. Note that it's easier to pull the box when it is in motion. So the friction decreases when the box is in motion and the friction when the box is in motion is called kinetic friction denoted by \({{f}_{k}}\). The kinetic friction is lesser than the static friction. Again the experiments show that kinetic friction is directly proportional to the normal force on the box, that is, \({{f}_{k}}\propto n\) and,
\[{{f}_{k}}={{\mu}_{k}}n \tag{2} \label{2}\]
In Eq. \eqref{2}, \({\mu}_{k}\) is a constant called the coefficient of kinetic friction. Here \({f}_{k}\) is approximately constant throughout the relative motion between the surfaces.
When two surfaces come in contact, the molecules on the surfaces form bonds with one another. Smother the surfaces, greater the number of molecules come in contact and more bonds are formed which increases the friction. The kinetic friction is approximately constant (not exactly constant) because the bonds between the surfaces form and break during the motion.





