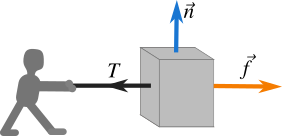
All forces have the same general nature which is push or pull. In Figure 1 a box is being pulled by a rope. The force exerted by a rope on a body is called tension \(T\). It also has opposite friction force \(\vec f\). The force the surface exerts perpendicular to the surface is called normal force, \(\vec n\).

A book of weight \(\vec{w}\) is on a surface of a table as shown in Figure 2. The book exerts a force equal to its weight on the surface of the table and in return the surface also applies the same magnitude of force on the book. Here the force exerted by the book is its weight but the force exerted by the surface is normal force \(\vec{n}\).

Figure 1 A person pulls a box with a rope.
Figure 2 A book on a table.
Figure 3 A box on an inclined plane. The net force on the box is zero, i.e. the box is in equilibrium condition.

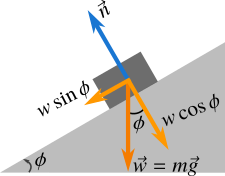
In Figure 3 a box is on an inclined plane. The weight of the box \(\vec{w}=m\vec{g}\) is vertically downwards and the normal force \(\vec{n}\) the surface exerts on the box is perpendicular to the inclined plane. In this situation the weight has two components; one is perpendicular to the inclined plane and another is parallel to the inclined plane.

The perpendicular component \({{w}_{\bot }}=w\cos \phi \) is balanced by the normal force \(\vec{n}\) and the parallel component \({{w}_{\parallel }}=w\sin \phi \) is balanced by the friction between the surfaces. Thus, the total net force acting on the box is zero and the box is in equilibrium condition.