In an adiabatic process no heat can enter or leave the system. Natural processes undergoing rapid expansion or compression behave like adiabatic processes as there is no appreciable heat flow into or out of the system. In rapid expansion or compression of a system there is not enough time to exchange heat with the surroundings. In rapid expansion of a natural process the system does work spending its internal energy and cools down. In rapid compression work is done on the system which increases the internal energy and the system warms up. Natural processes are found to be approximately in agreement with the ideal processes.
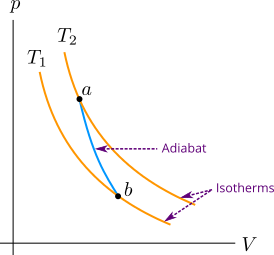
We already know that the internal energy of an adiabatic process of an ideal gas depends only on the temperature of the system. Increase in temperature means the increase in internal energy and decrease in temperature means the decrease in internal energy. In Figure 1 you can see \(p-V\) graph in which the adiabatic curve called adiabat between states \(a\) and \(b\) is steeper than isotherms. In adiabatic expansion the temperature of the system decreases and in adiabatic compression the temperature increases, and therefore the adiabat is steeper than the isotherms. Adiabatic expansion takes place from state \(a\) to state \(b\) and state \(b\) is on the isotherm at lower temperature \(T_1\) (temperature decreases).
What is the relationship of \(P\), \(V\) and \(T\) in adiabatic process?
In adiabatic process \(Q = 0\) and the infinitesimal form of the first law of thermodynamics gives \(dU = -dW\). Also we know that \(dW = pdV\) and \(dU = nC_VdT\). Note that \(dU = nC_VdT\) for any process as the internal energy depends only on the temperature of the system of ideal gas. Hence we can write the first law of thermodynamics for adiabatic process of ideal gas as
\[n{C_V}dT = - pdV \tag{1} \label{1}\]
We replace \(dT\) in the above equation by differentiating ideal gas equation and solving for \(dT\). We have ideal gas equation \(pV = nRT\) and differentiating both sides, we obtain,
\[pdV + Vdp = nRdT \tag{2} \label{2}\]
Solving for \(dT\) in Eq. \eqref{2} and putting its value in Eq. \eqref{1}, you'll finally obtain
\[({C_V} + R)pdV + {C_V}Vdp = 0 \tag{3} \label{3}\]
We know \(C_p = C_V + R\) and \(\gamma = C_p/C_V\) and rewriting the above equation we have,
\[\gamma \frac{{dV}}{V} + \frac{{dp}}{p} = 0 \tag{4} \label{4}\]
Integrating both sides of the above equation, you can find,
\[\begin{align*} \gamma \ln V + \ln p &= {\rm{constant}}\\ {\rm{or,}}\quad \ln p{V^\gamma } &= {\rm{constant}}\\ {\rm{or,}}\quad p{V^\gamma } &= {\rm{constant}} \tag{5} \label{5} \end{align*}\]
The Eq. \eqref{5} shows that the quantity \(p{V^\gamma }\) is constant in adiabatic process for an ideal gas. If \(p_1\) and \(V_1\) are the pressure and volume at initial state, and \(p_2\) and \(V_2\) are the pressure and volume at final state respectively, we have,
\[{p_1}V_1^\gamma = {p_2}V_2^\gamma \]
You can also express Eq. \eqref{5} in terms of volume and temperature. Eliminating \(p\) in Eq. \eqref{5} by \(p = nRT/V\) from ideal gas equation, you'll finally get:
\[T{V^{\gamma - 1}} = {\rm{constant}} \tag{6} \label{6}\]
Again if \(T_1\) and \(V_1\) are the the temperature and volume at initial state, and \(T_2\) and \(V_2\) are the temperature and volume at final state respectively, we have,
\[{T_1}V_1^{\gamma - 1} = {T_2}V_2^{\gamma - 1} \tag{7} \label{7}\]





