Let's consider a uniformly charged conducting sphere (Figure 1) of radius \(r\) and charge \(q\). We calculate the electric field produced by the charge on the sphere at various points inside or outside the sphere. First we calculate the electric field due to the charge distribution on the sphere outside the sphere and therefore enclose the sphere of radius \(r\) by a concentric Gaussian sphere of radius \(R\).
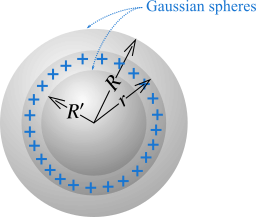
In each case we create a Gaussian surface, the point where we are calculating the electric field always lies on the Gaussian surface. Note that the sphere is symmetric and the electric field is radially outward at each point of the sphere. And we know from Gauss's law (applying Gauss's law),
\[{\rm{ }}\Phi = \oint {E\cos \theta dA} {\rm{ }} = \frac{q}{{{\epsilon_0}}}{\rm{ }}\]
Since the sphere is symmetric and the electric field is radially outward the electric field at every point on the Gaussian surface is uniform and perpendicular to the area element \(dA\). And \(\cos \theta =\cos 0=1\). So,
\[\begin{align*} \oint {EdA} {\rm{ }} &= \frac{q}{{{\epsilon_0}}}\\ {\rm{or, }}\quad E\oint {dA} &= \frac{q}{{{\epsilon_0}}}\\ {\rm{or,}}\quad {\rm{ }}EA &= \frac{q}{{{\epsilon_0}}}\\ {\rm{or,}}\quad E(4\pi {R^2}) &= \frac{q}{{{\epsilon_0}}}\\ \therefore E &= \frac{q}{{4\pi {\epsilon_0}{R^2}}} = k\frac{q}{{{R^2}}} \tag{1} \end{align*}\]
In this way we can determine the electric field at any distance \(R\) form the centre of the charged sphere. Our result shows that the electric field outside the sphere is the same as if all the charge were concentrated at the centre of the sphere, that is the electric field is the same as that of a point charge at the centre of the sphere.
Now we determine the electric field inside the charged sphere and in this case we make a Gaussian sphere of radius \(R'\) inside the sphere. In electrostatic situation i.e. charges not in motion the electric field inside the charged sphere is zero. The Gaussian surface which is inside the conductor (\(R' < r\)) encloses no charge and electric field inside the conductor is zero.
At the surface of the charged sphere, the Gaussian sphere has radius \(r\), the same as the radius of the charged sphere. Therefore the electric field is:
\[E = \frac{q}{{4\pi {\epsilon_0}{r^2}}}{\rm{ = }}k\frac{q}{{{r^2}}} \tag{2}\]
The electric field at the surface of the charged sphere is also the same as though all the charge were concentrated at the centre.
We recently determined the electric field of an uniformly charged conducting sphere. Now we determine the same thing for a uniformly charged insulating sphere where the charge is distributed uniformly throughout its volume.





