Let's consider a spherical shell which rotates about the x-axis with its centre at the origin of our coordinate system as shown in Figure 1. The radius of the spherical shell is \(R\). To find the moment of inertia of the spherical shell consider an infinitesimally small area element of the spherical shell of mass \(dm\), radius \(r\) and thickness \(dx\) at a distance \(x\) from the centre.
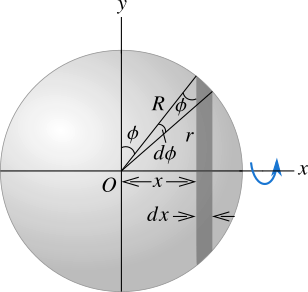
The area of the spherical shell is \(4\pi {R^2}\) and the area of the element is its circumference times its thickness which is \(2\pi r{\kern 1pt} dx\). Let \(M\) denotes the total mass of the spherical shell. The ratio of the mass of the element to the total mass of the spherical shell is equal to the ratio of the area of the element to the total area of the shell that is,
\[\begin{align*} \frac{{dm}}{M} &= \frac{{2\pi r{\kern 1pt} dx}}{{4\pi {R^2}}}\\ {\rm{or,}}\quad dm &= \frac{{rM{\kern 1pt} dx}}{{2{R^2}}} \end{align*}\]
In Figure 1 you can write \(x = R\sin \phi \) and if you differentiate \(x = R\sin \phi \) in both sides with respect to \(\phi\), you'll get \(dx/d\phi = R\cos \phi \). And \(r = R\cos \phi \), so you can write \(dx/d\phi = r\). Also \(dx = Rd\phi \) and we can find the mass of the element by using the above expression as
\[dm = \frac{M}{{2{R^2}}}\frac{{dx}}{{d\phi }}Rd\phi = \frac{M}{{2R}}dx\]
The moment of inertia of the element about the axis (in our case x-axis) through its centre perpendicular to its plane is the same as the moment of inertia of a thin ring about the axis through its centre perpendicular to its plane. You also know from Figure 4 that \(r = \sqrt {{R^2} - {x^2}} \). Therefore, the small moment of inertia of the element is,
\[\begin{align*} dI &= dm{\kern 1pt} {\kern 1pt} {r^2} = \left( {\frac{M}{{2R}}dx{\kern 1pt} } \right){\kern 1pt} {r^2}\\ or, \quad dI &= \left( {\frac{M}{{2R}}dx{\kern 1pt} } \right){\kern 1pt} ({R^2} - {x^2}) = \frac{M}{{2R}}({R^2} - {x^2})dx \end{align*}\]
The moment of inertia of the half of the spherical shell is found by integrating the moment of inertia of the element from \(0\) to \(R\). The total moment of inertia of the whole spherical shell is two times the moment of inertia of the half of the spherical shell. So the total moment of inertia is,
\[\begin{align*} I &= 2\int\limits_0^R {\frac{M}{{2R}}({R^2} - {x^2})dx = \frac{M}{R}\int\limits_0^R {({R^2} - {x^2})dx} } \\ {\rm{or,}}\quad I&= \frac{2}{3}M{R^2} \end{align*}\]





